TL-B 类型
此信息属于非常底层的内容,对新手来说可能难以理解。 因此,您可以稍后再阅读。
在本节中,我们将分析复杂和非传统的类型化语言二进制(TL-B)结构。开始之前,我们建议先阅读此文档,以更熟悉该主题。

Either
left$0 {X:Type} {Y:Type} value:X = Either X Y;
right$1 {X:Type} {Y:Type} value:Y = Either X Y;
Either类型用于可能出现两种结果类型之一的情况。在这种情况下,类型选择取决于所示的前缀位。如果前缀位是0,则序列化左类型,而如果使用1前缀位,则序列化右类型。
例如,在序列化消息时使用它,当消息体要么是主cell的一部分,要么链接到另一个cell。
Maybe
nothing$0 {X:Type} = Maybe X;
just$1 {X:Type} value:X = Maybe X;
Maybe类型与可选值一起使用。在这些情况下,如果第一位是0,则不会序列化该值(实际上被跳过),而如果值是1,则会被序列化。
Both
pair$_ {X:Type} {Y:Type} first:X second:Y = Both X Y;
Both类型变体仅与普通对一起使用,两种类型依次序列化,没有条件。
Unary
Unary函数类型通常用于动态大小的结构,例如hml_short。
Unary提供两个主要选项:
unary_zero$0 = Unary ~0;
unary_succ$1 {n:#} x:(Unary ~n) = Unary ~(n + 1);
Unary序列化
通常,使用unary_zero变体相当简单:如果第一位是0,则Unary反序列化的结果为0。
然而,unary_succ变体更复杂,因为它是递归加载的,具有~(n + 1)的值。这意味着它会顺序调用自身,直到达到unary_zero。换句话说,所需的值将等于一连串单位的数量。
例如,让我们分析位串110的序列化。
调用链如下:
unary_succ$1 -> unary_succ$1 -> unary_zero$0
一旦到达unary_zero,值就会返回到序列化位串的末尾,类似于递归函数调用。
现在,为了更清楚地理解结果,让我们检索返回值路径,显示如下:
0 -> ~(0 + 1) -> ~(1 + 1) -> 2,这意味着我们将110序列化为Unary 2。
Unary反序列化
假设我们有Foo类型:
foo$_ u:(Unary 2) = Foo;
根据上述内容,Foo将被反序列化为:
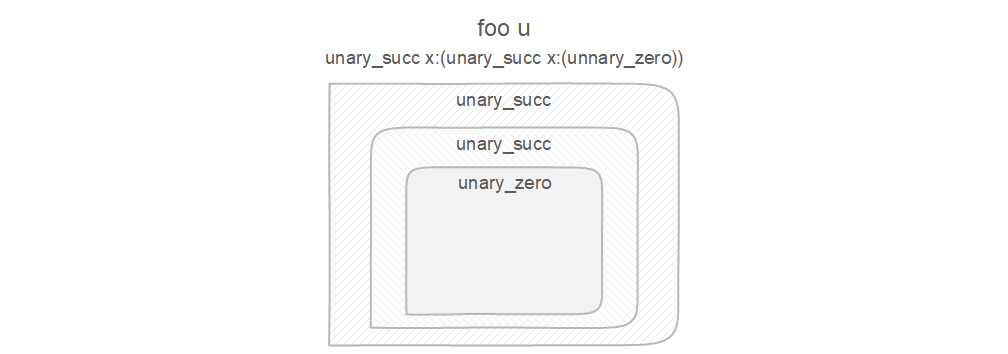
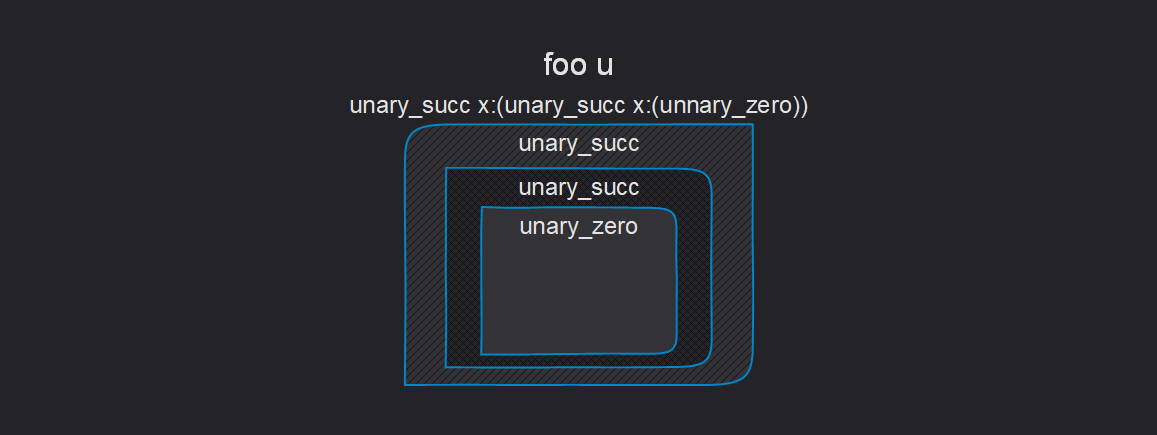
foo u:(unary_succ x:(unary_succ x:(unnary_zero)))
Hashmap
Hashmap复杂类型用于存储FunC智能合约代码中的字典(dict)。
以下TL-B结构用于序列化具有固定键长度的Hashmap:
hm_edge#_ {n:#} {X:Type} {l:#} {m:#} label:(HmLabel ~l n)
{n = (~m) + l} node:(HashmapNode m X) = Hashmap n X;
hmn_leaf#_ {X:Type} value:X = HashmapNode 0 X;
hmn_fork#_ {n:#} {X:Type} left:^(Hashmap n X)
right:^(Hashmap n X) = HashmapNode (n + 1) X;
hml_short$0 {m:#} {n:#} len:(Unary ~n) {n <= m} s:(n * Bit) = HmLabel ~n m;
hml_long$10 {m:#} n:(#<= m) s:(n * Bit) = HmLabel ~n m;
hml_same$11 {m:#} v:Bit n:(#<= m) = HmLabel ~n m;
unary_zero$0 = Unary ~0;
unary_succ$1 {n:#} x:(Unary ~n) = Unary ~(n + 1);
hme_empty$0 {n:#} {X:Type} = HashmapE n X;
hme_root$1 {n:#} {X:Type} root:^(Hashmap n X) = HashmapE n X;
这意味着根结构使用HashmapE及其两种状态之一:包括hme_empty或hme_root。
Hashmap解析示例
例如,考虑以下以二进制形式给出的Cell。
1[1] -> {
2[00] -> {
7[1001000] -> {
25[1010000010000001100001001],
25[1010000010000000001101111]
},
28[1011100000000000001100001001]
}
}
此Cell使用了HashmapE结构类型,并具有8位键大小,其值使用uint16数字框架(HashmapE 8 uint16)。HashmapE使用3种不同的键类型:
1 = 777
17 = 111
128 = 777
为了解析此Hashmap,我们需要预先知道使用哪种结构类型,hme_empty还是hme_root。这是通过识别正确前缀来确定的。hme empty变体使用一个位0(hme_empty$0),而hme root使用一个位1(hme_root$1)。读取第一位后,确定它等于一(1[1]),意味着它是hme_root变体。
现在,让我们用已知值填充结构变量,初始结果为:
hme_root$1 {n:#} {X:Type} root:^(Hashmap 8 uint16) = HashmapE 8 uint16;
这里已经读取了一位前缀,而{}中的条件不需要读取。条件{n:#}表示n是任何uint32数字,而{X:Type}表示X可以使用任何类型。
接下来需要读取的部分是root:^(Hashmap 8 uint16),而^符号表示必须加载的链接。
2[00] -> {
7[1001000] -> {
25[1010000010000001100001001],
25[1010000010000000001101111]
},
28[1011100000000000001100001001]
}
初始化分支解析
根据我们的架构,这是正确的Hashmap 8 uint16结构。接下来,我们用已知的值填充它,并得到如下结果:
hm_edge#_ {n:#} {X:Type} {l:#} {m:#} label:(HmLabel ~l 8)
{8 = (~m) + l} node:(HashmapNode m uint16) = Hashmap 8 uint16;
如上所示,现在出现了条件变量{l:#}和{m:#},但我们不知道这两个变量的值。此外,在读取相应的label之后,很明显n涉及等式{n = (~m) + l},在这种情况下我们计算l和m,符号~告诉我们结果值。
为了确定l的值,我们必须加载label:(HmLabel ~l uint16)序列。如下所示,HmLabel有三种基本结构选项:
hml_short$0 {m:#} {n:#} len:(Unary ~n) {n <= m} s:(n * Bit) = HmLabel ~n m;
hml_long$10 {m:#} n:(#<= m) s:(n * Bit) = HmLabel ~n m;
hml_same$11 {m:#} v:Bit n:(#<= m) = HmLabel ~n m;
每个选项都由相应的前缀确定。目前,我们的根cell由两个零位组成,显示为:(2[00])。因此,唯一合理的选项是以0开头的前缀hml_short$0。
用已知值填充hml_short:
hml_short$0 {m:#} {n:#} len:(Unary ~n) {n <= 8} s:(n * Bit) = HmLabel ~n 8
在这种情况下,我们不知道n的值,但由于它有一个~字符,可以计算它。为此,我们加载len:(Unary ~n),关于Unary的更多信息。
在这种情况下,我们从2[00]开始,但在定义了HmLabel类型之后,两个位中只剩下一个。
因此,我们加载它并看到它的值是0,这意味着它显然使用了unary_zero$0变体。这意味着使用HmLabel变体的n值为零。
接下来,需要使用计算出的n值完成hml_short变体序列:
hml_short$0 {m:#} {n:#} len:0 {n <= 8} s:(0 * Bit) = HmLabel 0 8
结果我们得到一个空的HmLabel,表示为s = 0,因此没有什么可以下载的。
接下来,我们用计算出的l值补充我们的结构,如下所示:
hm_edge#_ {n:#} {X:Type} {l:0} {m:#} label:(HmLabel 0 8)
{8 = (~m) + 0} node:(HashmapNode m uint16) = Hashmap 8 uint16;
现在我们已经计算出l的值,我们可以使用等式n = (~m) + 0来计算m,即m = n - 0,m = n = 8。
确定所有未知值后,现在可以加载node:(HashmapNode 8 uint16)。
至于HashmapNode,我们有以下选项:
hmn_leaf#_ {X:Type} value:X = HashmapNode 0 X;
hmn_fork#_ {n:#} {X:Type} left:^(Hashmap n X)
right:^(Hashmap n X) = HashmapNode (n + 1) X;
在这种情况下,我们不
是通过前缀来确定选项,而是通过参数来确定。这意味着如果n = 0,则正确的最终结果将是hmn_leaf或hmn_fork。在这个例子中,结果是n = 8(hmn_fork变体)。我们使用hmn_fork变体,并填入已知的值:
hmn_fork#_ {n:#} {X:uint16} left:^(Hashmap n uint16)
right:^(Hashmap n uint16) = HashmapNode (n + 1) uint16;
输入已知值后,我们必须计算HashmapNode (n + 1) uint16。这意味着n的结果值必须等于我们的参数,即8。
要计算本地n值,我们需要使用以下公式计算:n = (n_local + 1) -> n_local = (n - 1) -> n_local = (8 - 1) -> n_local = 7。
hmn_fork#_ {n:#} {X:uint16} left:^(Hashmap 7 uint16)
right:^(Hashmap 7 uint16) = HashmapNode (7 + 1) uint16;
现在我们知道了上述公式是必需的,获取最终结果就很简单了。 接下来我们加载左右分支,并对每个后续分支重复该过程。
分析加载的Hashmap值
继续前面的例子,让我们来看看加载分支的过程是如何工作的(对于dict值),即28[1011100000000000001100001001]
最终结果再次成为hm_edge,接下来的步骤是按照以下方式用正确的已知值填充序列:
hm_edge#_ {n:#} {X:Type} {l:#} {m:#} label:(HmLabel ~l 7)
{7 = (~m) + l} node:(HashmapNode m uint16) = Hashmap 7 uint16;
接下来使用HmLabel变体加载HmLabel响应,因为前缀是10。
hml_long$10 {m:#} n:(#<= m) s:(n * Bit) = HmLabel ~n m;
现在,让我们填充序列:
hml_long$10 {m:#} n:(#<= 7) s:(n * Bit) = HmLabel ~n 7;
新构造 - n:(#<= 7),清楚地表示一个与数字7对应的大小值,实际上是这个数字+1的log2。但为了简单起见,我们可以计算写数字7需要的位数。
相关地,数字7的二进制形式是111;因此需要3位,意味着n = 3的值。
hml_long$10 {m:#} n:(## 3) s:(n * Bit) = HmLabel ~n 7;
接下来我们将n加载到序列中,最终结果为111,如上所述,这与7相符。接下来,我们将s加载到序列中,7位 - 0000000。记住,s是键的一部分。
接下来我们回到序列的顶部并填充结果的l:
hm_edge#_ {n:#} {X:Type} {l:#} {m:#} label:(HmLabel 7 7)
{7 = (~m) + 7} node:(HashmapNode m uint16) = Hashmap 7 uint16;
然后我们计算m的值,m = 7 - 7,因此m的值为0。
由于m的值为0,该结构非常适合用于HashmapNode:
hmn_leaf#_ {X:Type} value:X = HashmapNode 0 X;
接下来我们替换我们的uint16类型并加载值。剩余的16位0000001100001001以十进制形式为777,因此这就是我们的值。
现在让我们恢复键,我们必须将之前计算的所有键部分的有序列表组合起来。两个相关的键部分根据使用的分支类型合并为一位。对于右分支,添加‘1’位,对于左分支添加‘0’位。如果上面有完整的HmLabel,则将其位添加到键中。
在这个特定的例子中,从HmLabel中取出7位0000000,并在零序列之前添加‘1’位,因为该值是从右分支获得的。最终结果是总共8位或10000000,意味着键值等于128。
其他Hashmap类型
现在我们已经讨论了Hashmaps及如何加载标准化的Hashmap类型,让我们解释其他Hashmap类型是如何工作的。
HashmapAugE
ahm_edge#_ {n:#} {X:Type} {Y:Type} {l:#} {m:#}
label:(HmLabel ~l n) {n = (~m) + l}
node:(HashmapAugNode m X Y) = HashmapAug n X Y;
ahmn_leaf#_ {X:Type} {Y:Type} extra:Y value:X = HashmapAugNode 0 X Y;
ahmn_fork#_ {n:#} {X:Type} {Y:Type} left:^(HashmapAug n X Y)
right:^(HashmapAug n X Y) extra:Y = HashmapAugNode (n + 1) X Y;
ahme_empty$0 {n:#} {X:Type} {Y:Type} extra:Y
= HashmapAugE n X Y;
ahme_root$1 {n:#} {X:Type} {Y:Type} root:^(HashmapAug n X Y)
extra:Y = HashmapAugE n X Y;
HashmapAugE与普通Hashmap的主要区别在于每个节点(不仅仅是带有值的叶子)都有一个extra:Y字段。
PfxHashmap
phm_edge#_ {n:#} {X:Type} {l:#} {m:#} label:(HmLabel ~l n)
{n = (~m) + l} node:(PfxHashmapNode m X)
= PfxHashmap n X;
phmn_leaf$0 {n:#} {X:Type} value:X = PfxHashmapNode n X;
phmn_fork$1 {n:#} {X:Type} left:^(PfxHashmap n X)
right:^(PfxHashmap n X) = PfxHashmapNode (n + 1) X;
phme_empty$0 {n:#} {X:Type} = PfxHashmapE n X;
phme_root$1 {n:#} {X:Type} root:^(PfxHashmap n X)
= PfxHashmapE n X;
PfxHashmap与普通Hashmap的主要区别在于它能够存储不同键长,这是由于存在phmn_leaf$0和phmn_fork$1节点。
VarHashmap
vhm_edge#_ {n:#} {X:Type} {l:#} {m:#} label:(HmLabel ~l n)
{n = (~m) + l} node:(VarHashmapNode m X)
= VarHashmap n X;
vhmn_leaf$00 {n:#} {X:Type} value:X = VarHashmapNode n X;
vhmn_fork$01 {n:#} {X:Type} left:^(VarHashmap n X)
right:^(VarHashmap n X) value:(Maybe X)
= VarHashmapNode (n + 1) X;
vhmn_cont$1 {n:#} {X:Type} branch:Bit child:^(VarHashmap n X)
value:X = VarHashmapNode (n + 1) X;
// nothing$0 {X:Type} = Maybe X;
// just$1 {X:Type} value
:X = Maybe X;
vhme_empty$0 {n:#} {X:Type} = VarHashmapE n X;
vhme_root$1 {n:#} {X:Type} root:^(VarHashmap n X)
= VarHashmapE n X;
VarHashmap与普通Hashmap的主要区别在于它能够存储不同键长,这是由于存在vhmn_leaf$00和vhmn_fork$01节点。此外,VarHashmap能够在vhmn_cont$1的代价下形成共同值前缀(子映射)。
BinTree
bta_leaf$0 {X:Type} {Y:Type} extra:Y leaf:X = BinTreeAug X Y;
bta_fork$1 {X:Type} {Y:Type} left:^(BinTreeAug X Y)
right:^(BinTreeAug X Y) extra:Y = BinTreeAug X Y;
二叉树键生成机制与标准化Hashmap框架类似,但不使用标签,只包括分支前缀。
地址
TON地址是使用TL-B StateInit结构通过sha256哈希机制形成的。这意味着地址可以在网络合约部署之前计算出来。
序列化
标准地址,例如EQBL2_3lMiyywU17g-or8N7v9hDmPCpttzBPE2isF2GTzpK4,使用base64 uri对字节进行编码。通常它们长度为36字节,其中最后两个字节是使用XMODEM表计算的crc16校验和,而第一个字节表示标志,第二个表示工作链。中间的32字节是地址本身的数据(也称为AccountID),通常在诸如int256之类的架构中表示。
参考
这里是Oleg Baranov的原文链接。